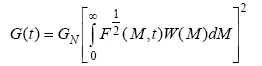
| Overview |
| Suggested Use of MWD |
| Using the MWD |
| Running the Optimizer Algorithm |
| Viewing the Results |
| Material Database |
| Notes on Calculation of MWD |
| References |
This function is designed to calculate the Molecular Weight (Mw) and Molecular Weight Distribution (MWD) of a material from dynamic mechanical frequency sweep data (G'[w] and G"[w]) by synthesizing a distribution based on material properties and an estimate for Mw and MWD. Dynamic data are then calculated from this distribution and overlaid with the experimental data to determine how closely the two sets of data agree with one other. The synthetic distribution can consist of between 1 and 10 separate components of the same material, each with its own Mw and MWD value. This allows for very complicated, asymmetric distributions to be synthesized, to better model the chemistry of real-world materials.
Iterative refinements to the estimated values of Mw and MWD may then be made either by the operator manually adjusting these parameters and looking for better agreement, or through the use of an automatic optimization function that adjusts these parameters by minimizing the numerical difference between the two data sets.
This function can also be used to calculate dynamic frequency sweep data, without starting from a reference set of data, and based only on a given Mw, MWD, and material parameters. See the section Notes on the Calculation of MWD for additional information on the calculations by this method.
The MWD function is designed to determine the molecular weight distribution of polymeric materials from the dynamic mechanical properties G'(w) and G"(w). The approach is based on a molecular model, the double reputation mixing rule, to calculate the MWD from the viscoelastic relaxation time spectrum.
The experimental frequency sweep data should contain data covering at least three decades of frequency, measured between the terminal region and rubbery plateau region for the polymer melt. One advantage to this approach is that it works with "incomplete" sets of data. Typically, the methods used to calculate MWD from rheology data require that a master curve be used that covers the range of viscoelasticity from the rubbery region all the way down into the terminal region. Since this function works by comparing sets of dynamic data over the same frequency range, it is possible to get accurate distribution information over a more narrow range of frequencies, though obviously having a wider range of frequencies (and therefore relaxation times) is always preferable.
This model used here is suitable only for homopolymers with either unimodal or bi (N-)modal distributions. In order for realistic values to be calculated, all of the rheological data must have been made in the region of linear viscoelasticity. The presence of additives in the sample may also affect the results. In general, any additive or morphological change that affects the rheological behavior will invalidate the results. Examples of types of additives causing problems include the presence of solvent molecules, plasticizers, fillers, and processing aids. Long-chain branching and residual crystallinity can also affect the results, as can the presence of ionic charges on the polymer.
Additives such as stabilizers and antioxidents should generally not cause a problem, because typically the concentration of these materials is not high enough to significantly change the rheology of the melt. The determination of the MWD from rheology is, in contrast to SEC, very sensitive to the high molecular contributions and, as such, a complementary and not a competitive technique.
The MWD function is available if a set of dynamic data is active (i.e. the current page contains G', G", and frequency data). To use MWD:
The user interface for calculating the MWD shows a plot on the right side with the experimental G’ and G” data, as well as the calculated data, based on the current default values. The format of the plot can be switched between the rheological data (G’, G”) and the molecular data, either the w(Mw ) or the w(Mw)*Mw.
The first step in using the MWD function is to select the Polymer Type to be used in the model. This designates a set of constants to be used for the calculation of the rheological properties based on the synthesized molecular weight distribution. TRIOS provides a built-in database of these parameters for some common commercial polymers. These constants can be viewed and edited. New materials can also be added to the database (see Material Database below).
The DataTemperature field is used to view or set the reference temperature for the calculation. In the case where data are being generated to match an existing data set, this value should correspond to the average temperature at which the data were run. This value is then used along with the material activation energy to shift the front factor used for mapping molecular weights to relaxation times.
This section is used to specify the parameters used for building the synthetic molecular weight distribution. The values specified are:
Log-normal (Wesslau) distribution is typical of addition and Ziegler-Natta catalyzed systems. The Schultz distribution is used with polymers produced via condensation reactions or with metallocene catalysts. These values can be changed by the user to create a desired distribution, or automatically updated by the MWD optimization engine to attempt to match the selected frequency sweep data.
Three different systems of distributions can be built:
Edit fields and spin buttons are used to change the values in both Unimodal and Bimodal distributions. N-Modal distributions are presented in the form of a table, and double-clicking on the parameter to modify can change the individual values. This brings up an edit field, allowing the parameter to be modified. Note that since the fractions in any multicomponent system must sum to 1.0, the value for the fraction of the last component is automatically set to enforce this rule.
The Copy and Paste functions in this section are used to store and retrieve a custom starting point for solutions. This allows users to always start the optimization calculations from the same set of parameters, which can produce more consistent results.
Prior to starting the calculation, a reasonable guess should be made for the Mw and MWD. If a bimodal model is used, then initial values should be provided for each component, as well as a value for the ratio of the two components. Providing reasonable estimates for these parameters allows the calculation to converge faster and decreases the possibility of the function falling into a local, non-optimal minima instead of the desired global minima that best fits the data.
The kernel used to model the rheological data based on the synthesized distribution can be adjusted by the settings in the Advanced Options section.
The Double Reptation model assumes that the stress relaxation modulus (G[t]) depends on the square root of the monodispersed relaxation function F1/2(Mw,t), whereas the Wt Average method assumes that this dependence is to the first power F(Mw,t).
Click Settings to display a dialog box containing additional advanced settings for MWD calculations. These include:
The section displays the results of the calculation, including the various moments of the distribution (Mn, Mw, Mz, Mz+1, and Mw/Mn), as well as an Error metric, which indicates how closely the generated data matches the experimental data. A value of NAN (a non-number) is displayed if there are no experimental data to match. This is a least-squares measurement of the agreement between the experimental data and the calculated G' and G" results. This can be used to guide the user in determining the optimum Mw and MWD values, since the smaller the value, the better the fit between the data sets.
Once the correct material database is selected and the initial values of the MWD to synthesize have been selected, start the optimization by clicking Optimize.
By closing the MWD user interface, the model curve for the storage and loss modulus are plotted on the active plot and the results stamped on the plot.
Click Edit in the Material section to open the material database. For each material type, the following model parameters are needed in order to obtain a correct molecular weight distribution.
Material parameters can be edited and saved when the form is closed normally (clicking OK). Cancel exits the form without saving the changes. If the database does not include the desired polymer type, a new material entry can be created and added to the material data base.
This function makes use of an algorithm and implementation developed by David Mead and his group at the University of Michigan, and is licensed to TA Instruments for incorporation in Orchestrator/TRIOS Software.
The quantitative relationship that relates the observed mechanical properties of a polydisperse melt and the underlying polymer structure is called a mixing rule. The mixing rule is a relatively simple mathematical approximation to a more complex molecular theory of polydispersity. The double reptation mixing rule used in the TA Orchestrator has the following mathematical structure:
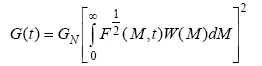
Here, G(t) is the relaxation modulus which can be determined from various linear viscoelasticity experiments, in the present implementation from G’(w) and G”(w). The function F1/2(M,t) is the monodisperse relaxation function which represents the time dependent fractional stress relaxation of a monodisperse polymer following a small step strain. W(M) is the weight based MWD, that is w(M)dM represents the weight fraction of material with molecular weights between M and M+dM. Physically, all components of the MWD will contribute to the modulus to some extent. The magnitude of each component's contribution to the stress will depend on the details of the interaction with the other molecules in the MWD.
To calculate an MWD for a given material using the equation above, it will be necessary to supply material dependent information to the application. Specifically, the plateau modulus GN and the form of the monodisperse relaxation function F1/2(M,t) must be supplied. The plateau modulus is tabulated in several references. The monodisperse relaxation function can take several forms. Generally, we shall use a single exponential form:
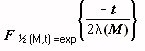
Here,l(M) is the characteristic relaxation time for the monodisperse system and K(T) is a coefficient (front factor) that depends on temperature. The exponent x is typically ~3.4 for flexible polymers. The Doi-Edwards terms are higher terms of the monodisperse relaxation function.